Resultan 2 Vektor Sejajar, Tegak Lurus dan Mengapit Sudut
https://www.fisikabc.com/2017/05/resultan-vektor-sejajar-tegak-lurus-mengapit-sudut.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Resultan Dua Vektor yang Sejajar atau Segaris
Perhatikan gambar ilustrasi di bawah ini. Dua orang anak yaitu Andan dan Akeb sedang menarik seorang anak berbadan tambun bernama Okta menggunakan seutas tali, namun ternyata sekeras apapun usaha Akeb dan Andan menarik tali, si Okta ternyata tidak bergerak sedikitpun. Menurut Anda mengapa hal ini bisa terjadi?
Ketiga vektor a, b dan c di atas jika dihubungkan jadi satu maka akan membentuk satu garis lurus seperti gambar di bawah ini.
Lalu bagaimana cara menentukan resultan dari dua vektor yang sejajar atau segaris? Resultan dari dua buah vektor yang sejajar ada 2 macam, yaitu resultan hasil penjumlahan dan resultan hasil pengurangan atau selisih.
R = |A + B|
Dan arah vektor resultannya adalah searah dengan kedua vektor tersebut.
Contoh soal penjumlahan vektor sejajar
Misalkan, Andi sedang bepergian mengelilingi kota Bandung dengan sepeda motor. Dua jam pertama, Andi bergerak lurus ke timur dan menempuh jarak sejauh 50 km. setelah istirahat secukupnya, Andi kembali melanjutkan perjalanan lurus ke timur sejauh 30 km lagi. Tentukan besar dan arah resultan perpindahan Andi!
Jawab:
#1 Penjumlahan dua vektor yang sejajar atau segaris
Dua vektor yang sejajar dapat dijumlahkan dengan syarat arah kedua vektor sama dengan kata lain kedua vektor adalah searah. Secara matematis, rumus besar resultan hasil penjumlahan vektor yang sejajar adalah sebagai berikut:R = |A + B|
Dan arah vektor resultannya adalah searah dengan kedua vektor tersebut.
Contoh soal penjumlahan vektor sejajar
Misalkan, Andi sedang bepergian mengelilingi kota Bandung dengan sepeda motor. Dua jam pertama, Andi bergerak lurus ke timur dan menempuh jarak sejauh 50 km. setelah istirahat secukupnya, Andi kembali melanjutkan perjalanan lurus ke timur sejauh 30 km lagi. Tentukan besar dan arah resultan perpindahan Andi!
Jawab:
Diketahui
perpindahan A = 50 km arah timur
perpindahan B = 30 km arah timut
maka R = |A + B|
R = |50 + 30| = 80
Jadi resultan perpindahan Andai adalah 80 km ke arah timur
#2 Pengurangan/selisih dua vektor yang sejajar atau segaris
Dua vektor yang sejajar dapat dikurangkan dengan syarat arah kedua vektor berlawnan dengan kata lain kedua vektor berlawanan arah. Secara matematis, rumus besar resultan hasil selisih vektor yang sejajar adalah sebagai berikut:
R = |A - B|
Dan arah vektor resultannya adalah searah dengan vektor terbesar.
Contoh soal pengurangan vektor sejajar
Sedikit berbeda dengan soal penjumlahan vektor tadi, misalkan, Andi telah menempuh jarak lurus 50 km ke arah timur, kemudian kembali lagi ke barat sejauh 70 km. Tentukan besar dan arah resultan perpindahan Andi!
Jawab:
perpindahan A = 50 km arah timur
perpindahan B = 70 km arah barat
maka R = |A - B|
R = |50 - 70| = 20
Jadi resultan perpindahan Andai adalah 20 km ke arah barat.
Perlu Anda ketahui bahwa, rumus resultan hasil penjumlahan dan pengurangan dua vektor sejajar di atas juga berlaku untuk tiga atau lebih vektor yang sejajar.
Lalu kembali lagi ke pertanyaan awal tadi, kenapa badan Okta tidak bergerak sedikitpun meski sudah ditarik oleh dua orang anak? Untuk menjawabnya kita analisis vektor-vektor yang bekerja pada gambar ilustrasi di atas.
Berdasarkan ilustrasi di atas, Akeb dan Andan mengerjakan gaya tarik ke kanan sebesar A dan B, sedangkan Okta mengerjakan gaya tarik ke kiri sebesar C. Jika vektor A dan B kita jumlahkan dan bandingkan dengan vektor C maka hasilnya seperti pada gambar di bawah ini
Kemungkinan besar yang menyebabkan badan Okta tidak bergerak adalah karena gaya tarik yang dikerjakan Akeb dan Andan terhadap tali sama dengan gaya tarik yang dikerjakan Okta terhadap tali. Sehingga nilai resultannya adalah nol. Secara matematis ditulis
A + B = C
R = |(A + B) -C| = 0
Resultan Dua Vektor yang Saling Tegak Lurus
Misalkan, Anda sedang memacu kendaraan Anda lurus ke timur sejauh 40 km. kemudian berbelok tegak lurus menuju utara sejauh 30 km. Secara grafis, perpindahan Anda seperti diperlihatkan pada gambar di bawah ini.
Besar resultan perpindahan r dapat diperoleh menggunakan Dalil Pytagoras, yaitu sebagai berikut:
r = √(x2 + y2) = √ (402 + 302) = √2.500 = 50 km
sedangkan arahnya ditentukan dengan menggunakan rumus tangen yaitu:
tan θ = y/x = 30/40 = ¾ → θ = arc tan (3/4) = 37o
jadi arah resultan vektornya adalah 37o terhadap sumbu X positif (atau 37o dari arah timur).
Dari contoh kasus tersebut, jika dua buah vektor A dan B saling tegak lurus akan menghasilkan vektor resultan R, yang besarnya resultan ditetukan dengan rumus sebagai berikut:
Sedangkan arah resultan dapat dicari dengan rumus atau persamaan berikut:
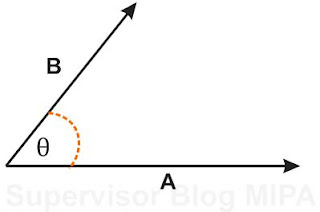
Resultan Dua Vektor yang Mengapit Sudut
Sekarang tinjau dua buah vektor A dan B dimana satu sama lain mengapit sudut seperti diperlihatkan seperti pada gambar di bawah ini:
Kemudian gambar vektor resultannya dapat diperoleh dengan menggunakan metode segitiga yaitu dengan cara menempatkan pangkal vektor B di ujung vektor A. Selanjutnya tarik garis dari titik pangkal vektor A ke titik ujung vektor B. vektor inilah yang dinamakan vektor R, resultan dari vektor A dan B. hasilnya seperti pada gambar berikut
Besar vektor resultan R dapat ditentukan secara analitis sebagai berikut. Perhatikan gambar di bawah ini.
Vektor C dan D diberikan sebagai alat bantu sehingga vektor A + C tegak lurus terhadap vektor D dan ketiganya membentuk resultan yang sama dengan resultan dari vektor A dan B yaitu R. Dengan menggunakan Dalil Pythagoras, besarnya vektor resultan R adalah
Selanjutnya dengan menggunakan Dalil Pythagoras, dari gambar di atas diperoleh
C2 + D2 = B2
Dan dari rumus trigonometri diperoleh:
Dengan memasukkan dua persamaan terakhir ke persamaan pertama, diperoleh besarnya vektor R, yaitu sebagai berikut:
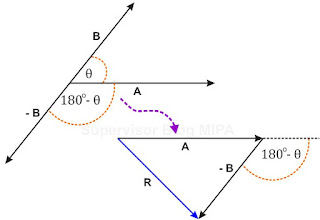
Selisih Dua Vektor yang Mengapit Sudut
Vektor A dan vektor –A, memiliki besar yang sama, yaitu |A| = |-A| = A, tetapi dengan arah yang berlawanan seperti pada gambar di atas. Selisih dari dua buah vektor, misalnya vektor A – B, secara grafis sama dengan jumlah antara vektor A dan vektor –B, seperti pada gambar di bawah ini. Secara matematis, vektor selisihnya ditulis R = A – B.
Secara analitis, besar vektor selisihnya ditentukan dari persamaan sebelumnya dengan mengganti θ dengan 180 - θ. Karena cos (180 - θ) = - cos θ, sehingga diperoleh:
Demikianlah artikel tentang cara menentukan vektor resultan dari 2 vektor yang sejajar, saling tegak lurus dan membentuk sudut. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.