Hukum Newton Pada Gerak Benda di Bidang Datar Kasar
https://www.fisikabc.com/2017/07/gerak-benda-pada-bidang-datar-kasar.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Pernahkah kalian menggelindingkan bola di lapangan rumput? Jika pernah, coba kalian amati gerak bola tersebut. Bola mula-mula bergerak mendatar dan setelah menempuh jarak tertentu, bola tersebut pasti berhenti. Kenapa bola bisa berhenti? Tentunya karena pengaruh gaya gesek yang arahnya berlawanan dengan arah gerak bola. Peristiwa menggelindingnya bola di lapangan rumput tersebut merupakan salah satu contoh penerapan Hukum Newton pada gerak benda di bidang datar kasar.
Pada kesempatan kali ini, penulis akan membahas aplikasi Hukum Newton pada gerak benda di bidang datar kasar dalam tiga kondisi atau keadaan yang berbeda. Tiga kondisi tersebut antara lain: benda yang didorong atau ditarik dengan gaya mendatar, benda yang ditarik dengan gaya miring ke atas dan benda yang didorong dengan gaya miring ke bawah.
Untuk menyelesaikan permasalah yang berhubungan dengan gerak benda pada bidang datar menggunakan Hukum Newton, ada beberapa catatan yang perlu kalian perhatikan, yaitu:
•Pertama, gambarlah diagram secara terpisah yang menggambarkan semua gaya yang bekerja pada benda (gambar diagram bebas).
•Kedua, gaya yang searah dengan perpindahan benda dianggap positif, sedangkan gaya yang berlawanan arah dengan perpindahan benda dianggap negatif.
|
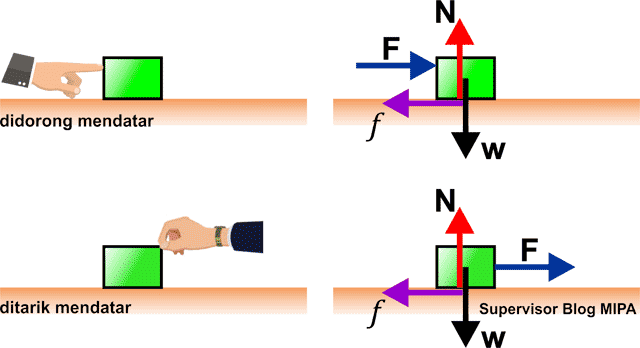
#1 Benda Didorong atau Ditarik dengan Gaya Mendatar
Sebuah benda terletak pada bidang datar kasar didorong atau ditarik dengan gaya sebesar F diperlihatkan pada gambar di atas. Ketika kita mendorong atau menarik suatu benda secara horizontal ke kanan misalnya, memiliki konsep gerak yang sama dimana gaya F yang dialami benda adalah sama-sama ke kanan sehingga persamaa gerak yang dihasilkan akan sama.
Karena bidang kasar, maka ada dua kemungkinan yang dialami benda, yaitu benda diam dan benda bergerak horisontal (sejajar bidang). Pada gambar di atas, arah gaya tarik atau gaya dorong adalah ke kanan sehingga apabila benda bergerak maka arahnya juga ke kanan. Dengan demikian arah perpindahan benda juga ke kanan. Oleh karena itu gaya yang arahnya ke kanan bernilai positif dan yang ke kiri bernilai negatif.
Benda Diam
Apabila benda setelah diberi gaya F mendatar pada bidang kasar, keadaan benda tetap diam maka gaya gesek yang bekerja pada benda adalah gaya gesek statis (fs). Jika koefisien gesek statis adalah μs maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – w = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – w = 0
N = w
Dengan demikian besar gaya normal akan sama dengan berat benda, sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = w = mg
|
Resultan gaya pada sumbu-X
ΣFX = ma
F – fs = ma
F – μsN = ma
Karena N = mg, maka besar gaya geseknya adalah f = fs = μsmg sehingga
F – μsmg = ma
Karena benda diam, maka a = 0
F – μsmg = 0
F = μsmg
Dengan demikian, persamaan gerak benda yang ditarik atau didorong dengan gaya F mendatar pada bidang datar kasar namun benda tetap diam adalah sebagai berikut.
F = μsmg
|
Benda Bergerak Horizontal atau Sejajar Bidang
Apabila setelah diberi gaya tarik atau gaya dorong F benda bergerak, maka benda mengalami percepatan (a ≠ 0) dan gaya gesek yang bekerja pada benda adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetik antara permukaan benda dengan bidang adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – w = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – w = 0
N = w
Dengan demikian besar gaya normal akan sama dengan gaya berat benda (benda diam atau bergerak tidak mempengaruhi gaya normal), sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = w = mg
|
Resultan gaya pada sumbu-X
ΣFX = ma
F – fk = ma
F – μkN = ma
Karena N = mg maka besar gaya geseknya adalah f = fk = μkmg sehingga
F – μkmg = ma
F = ma + μkmg
F = m (a + μkg)
Dengan demikian, persamaan gerak benda yang ditarik atau didorong dengan gaya F mendatar pada bidang datar kasar dan benda bergerak adalah sebagai berikut.
F = m (a + μkg)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tarik atau dorong (N)
|
f
|
=
|
Gaya gesek (N)
|
μs
|
=
|
Koefisien gesek statis
|
μk
|
=
|
Koefisien gesek kinetis
|
m
|
=
|
Massa benda (kg)
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#2 Benda Ditarik dengan Gaya Miring ke Atas
Suatu benda yang terletak pada bidang datar kasar ditarik dengan gaya miring ke atas ditampilan pada gambar di atas. Karena vektor F membentuk sudut sebesar α terhadap arah mendatar, maka F dapat diproyeksikan terhadap sumbu-X dan sumbu-Y sehingga dihasilkan gaya F cos α yang arahnya ke kanan dan gaya F sin α yang arahnya ke atas.
Pada kondisi ini ada tiga kemungkinan gerak benda yaitu benda diam, benda bergerak horizontal atau benda mengalami gerak vertikal ke atas. Namun kita hanya akan membahas dua kemungkinan saja, yaitu kemungkinan benda diam dan bergerak horizontal, karena dua kemungkinan inilah yang sering muncul dalam soal fisika khususnya dinamika.
Pada kondisi ini ada tiga kemungkinan gerak benda yaitu benda diam, benda bergerak horizontal atau benda mengalami gerak vertikal ke atas. Namun kita hanya akan membahas dua kemungkinan saja, yaitu kemungkinan benda diam dan bergerak horizontal, karena dua kemungkinan inilah yang sering muncul dalam soal fisika khususnya dinamika.
Benda Diam
Pada benda yang diam di atas bidang datar kasar, selalu bekerja gaya gesek statis (fs). Jika koefisien gesek statis adalah μs maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N + F sin α – w = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N + F sin α – w = 0
N = w – F sin α
N = mg – F sin α
Dengan demikian besar gaya normal akan sama dengan berat benda dikurang proyeksi gaya F pada sumbu-Y, sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = mg – F sin α
|
Resultan gaya pada sumbu-X
ΣFX = ma
F cos α – fs = ma
F cos α – μsN = ma
Karena N = mg – F sin α, maka besar gaya geseknya adalah f = fs = μs(mg – F sin α) sehingga
F – μs(mg – F sin α) = ma
Karena benda diam, maka a = 0
F – μs(mg – F sin α) = 0
F = μs(mg – F sin α)
Dengan demikian, persamaan gerak benda yang ditarik dengan gaya F miring ke atas pada bidang datar kasar namun benda tetap diam adalah sebagai berikut.
F = μs(mg – F sin α)
|
Benda Bergerak Horizontal atau Sejajar Bidang
Gaya gesek yang bekerja pada benda yang bergerak pada bidang datar kasar adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetik antara permukaan benda dengan bidang adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
Resultan gaya pada sumbu-Y untuk benda yang bergerak horisontal adalah sama dengan resultan gaya pada sumbu-Y untuk benda diam pada kondisi benda yang ditarik miring ke atas, sehingga persamaan gaya normalnya adalah sebagai berikut.
N = mg – F sin α
Resultan gaya pada sumbu-X
ΣFX = ma
F cos α – fk = ma
F cos α – μkN = ma
Karena N = mg – F sin α, maka besar gaya geseknya adalah f = fk = μk(mg – F sin α) sehingga
F – μk(mg – F sin α) = ma
F – μkmg + μkF sin α = ma
F – ma = μkmg – μkF sin α
F – ma = μk (mg – F sin α)
Dengan demikian, persamaan gerak benda yang ditarik dengan gaya F miring ke atas pada bidang datar kasar dan benda bergerak adalah sebagai berikut.
F – ma = μk (mg – F sin α)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tarik (N)
|
f
|
=
|
Gaya gesek (N)
|
μs
|
=
|
Koefisien gesek statis
|
μk
|
=
|
Koefisien gesek kinetis
|
α
|
=
|
Sudut kemiringan gaya tarik terhadap bidang horizontal
|
m
|
=
|
Massa benda (kg)
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#3 Benda DiDorong dengan Gaya Miring ke Bawah
Sebuah benda berada di atas bidang datar kasar didorong miring ke bawah ditunjukkan pada gambar di atas. Karena miring, vektor gaya F membentuk sudut sebesar α terhadap arah horizontal maka dengan menggunakan metode penguraian vektor kita dapatkan vektor F sin α (hasil proyeksi F terhadap sumbu-Y) dan vektor F cos α (hasil proyeksi F terhadap sumbu-X).
Jika kita analisis garis-garis gaya yang bekerja pada benda, maka terdapat tiga kemungkinan gerak benda. Tiga kemungkinan tersebut adalah benda diam, bergerak horizontal (sejajar bidang) atau benda mengalami gerak vertikal ke bawah. Namun kemungkinan benda bergerak vertikal ke bawah itu sangat kecil sekali atau sangat jarang terjadi sehingga kita hanya akan membahas dua kemungkinan saja yaitu benda diam dan bergerak mendatar.
Benda Diam
Pada benda yang diam di atas bidang datar kasar, selalu bekerja gaya gesek statis (fs). Jika koefisien gesek statis adalah μs maka persamaan Hukum Newton pada keadaan ini adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – F sin α – w = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – F sin α – w = 0
N = w + F sin α
N = mg + F sin α
Dengan demikian besar gaya normal akan sama dengan berat benda ditambah proyeksi gaya F pada sumbu-Y, sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = mg + F sin α
|
Resultan gaya pada sumbu-X
ΣFX = ma
F cos α – fs = ma
F cos α – μsN = ma
Karena N = mg + F sin α, maka besar gaya geseknya adalah f = fs = μs(mg + F sin α) sehingga
F – μs(mg + F sin α) = ma
Karena benda diam, maka a = 0
F – μs(mg + F sin α) = 0
F = μs(mg + F sin α)
Dengan demikian, persamaan gerak benda yang didorong dengan gaya F miring ke bawah pada bidang datar kasar namun benda tetap diam adalah sebagai berikut.
F = μs(mg + F sin α)
|
Benda Bergerak Horizontal atau Sejajar Bidang
Gaya gesek yang bekerja pada benda yang bergerak pada bidang datar kasar adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetik antara permukaan benda dengan bidang adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
Resultan gaya pada sumbu-Y untuk benda yang bergerak horisontal adalah sama dengan resultan gaya pada sumbu-Y untuk benda diam pada kondisi benda yang didorong miring ke bawah, sehingga persamaan gaya normalnya adalah sebagai berikut.
N = mg + F sin α
Resultan gaya pada sumbu-X
ΣFX = ma
F cos α – fk = ma
F cos α – μkN = ma
Karena N = mg + F sin α, maka besar gaya geseknya adalah f = fk = μk(mg + F sin α) sehingga
F – μk(mg + F sin α) = ma
F – μkmg – μkF sin α = ma
F – ma = μkmg + μkF sin α
F – ma = μk (mg + F sin α)
Dengan demikian, persamaan gerak benda yang didorong dengan gaya F miring ke bawah pada bidang datar kasar dan benda bergerak adalah sebagai berikut.
F – ma = μk (mg + F sin α)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya dorong (N)
|
f
|
=
|
Gaya gesek (N)
|
μs
|
=
|
Koefisien gesek statis
|
μk
|
=
|
Koefisien gesek kinetis
|
α
|
=
|
Sudut kemiringan gaya tarik terhadap bidang horizontal
|
m
|
=
|
Massa benda (kg)
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
Demikianlah artikel tentang penerapan atau aplikasi Hukum Newton pada gerak benda di bidang datar kasar beserta gambar dan penjelasannya. Untuk penerapan Hukum Newton pada bidang licin silahkan kalian simak artikel tentang Hukum Newton pada gerak benda di bidang datar licin. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di atikel berikutnya.


Kak, pd rumus nomor #3 adalah rumus tentang Benda DiDorong dengan Gaya Miring ke Bawah. Tapi saat kesimpulan rumus pada benda didorong dengan gaya miring kebawah malah tertulis persamaan gerak benda yang ditarik dengan gaya F miring ke atas pada bidang datar kasar namun benda tetap diam adalah sebagai berikut.
ReplyDeleteTerimakasih kak fen atas koreksinya, artikel akan kami perbaiki segera.
Delete