Contoh Soal dan Pembahasan Tentang Gaya Kontak Beserta Gambar Ilustrasi
https://www.fisikabc.com/2017/09/contoh-soal-gaya-kontak-dinamika-translasi.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Pada kesempatan kali ini kita akan membahas tentang beberapa contoh soal tentang gaya aksi-reaksi atau sering disebut sebagai gaya kontak. Menurut Hukum III Newton, gaya kontak merupakan gaya yang timbul akibat dua objek saling berinteraksi di mana objek pertama memberikan gaya aksi ke pada objek kedua dan sebagai balasannya, objek kedua memberikan gaya reaksi ke pada objek pertama.
Model soal yang akan kita bahas adalah beberapa objek yang saling bersentuhan di bidang miring dan juga bidang datar. Oleh karena itu, kita memperhitungkan keadaan permukaan bidang tersebut. Jika bidang licin, besar gaya kontak tidak dipengaruhi oleh gaya gesek dan sebaliknya, apabila bidang kasar maka besar gaya kontak dipengaruhi oleh gaya gesek.
Untuk itu, sebelum masuk ke pembahasan soal, ada baiknya kita pelajari terlebih dahulu mengenai konsep Hukum Newton tentang gerak benda dan juga konsep gaya gesek. Silahkan kalian pahami baik-baik ringkasan konsep berikut ini.
Konsep Hukum Newton
Hukum I Newton
|
Hukum II Newton
|
Hukum III Newton
|
ΣF = 0
|
ΣF = ma
|
Faksi = −Freaksi
|
Keadaan benda:
■ diam (v = 0 m/s)
|
Keadaan benda:
|
Sifat gaya aksi reaksi:
■ sama besar
■ berlawanan arah
■ terjadi pada 2 objek berbeda
|
Penjelasan lengkap mengenai Hukum Newton, baca artikel tentang: Bunyi dan Rumus Hukum Newton I, II, dan III Beserta Contohnya.
Konsep Gaya Gesek
Gaya Gesek Statis
|
Gaya Gesek Kinetis
|
fs = μs N
|
fk = μk N
|
Bekerja pada benda:
■ diam (v = 0 m/s)
■ tepat akan bergerak (fs maksimum)
|
Bekerja pada benda:
■ bergerak (baik GLB maupun GLBB)
|
Penjelasan lengkap mengenai gaya gesek, baca artikel tentang: Definisi, Sifat, Jenis, Rumus dan Contoh Soal tentang Gaya Gesek.
Hubungan Gaya Gesek dan Gerak Benda
Besar Gaya Luar
|
Keadaan Benda
|
Jika F < fs maksimum
|
Diam, berlaku Hukum I Newton
|
Jika F > fs maksimum
|
Bergerak, berlaku Hukum II Newton dan bekerja gaya gesek kinetik (fk)
|
Oke, jika kalian sudah paham mengenai konsep Hukum Newton dan gaya gesek, kini saatnya kita bahas beberapa soal tentang gaya aksi-reaksi atau gaya kontak. Simak baik-baik uraian berikut ini.
Contoh Soal #1
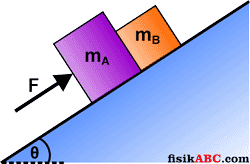
Balok A dan balok B terletak di atas permukaan bidang miring licin dengan sudut kemiringan 37°. Massa balok A 40 kg dan massa balok B 20 kg. Kemudian balok A didorong dengan gaya F sebesar 480 N seperti yang diperlihatkan pada gambar di bawah ini. Tentukan besar percepatan gerak kedua balok dan juga gaya kontak antara balok A dan balok B.
Jawab
Diketahui:
mA = 40 kg
mB = 20 kg
F = 480 N
θ = 37°
g = 10 m/s2
Ditanyakan: Percepatan dan gaya kontak.
Langkah pertama adalah menggambarkan diagram gaya yang bekerja pada masing-masing balok secara terpisah untuk mempermudah membedakan gaya-gaya mana yang bekerja pada kedua balok. Perhatikan gambar di bawah ini.
FAB adalah gaya aksi yang diberikan balok A kepada balok B, sedangkan FBA adalah gaya reaksi yang diberikan balok B kepada balok A. Kedua gaya tersebut merupakan gaya kontak yang besarnya sama. Lalu untuk menentukan besar percepatan kedua balok dan juga gaya kontak, kita tinjau persamaan gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.
■ Tinjau Balok A
■ Tinjau Balok A
Karena bidang miring licin maka tidak ada gaya gesek yang bekerja, sehingga resultan gaya pada sumbu-Y tidak perlu diuraikan.
ΣFX = ma
F – wA sin θ – FBA = mAa
F – mAg sin θ – FBA = mAa ............... Pers. (1)
■ Tinjau Balok B
ΣFX = ma
FAB – wA sin θ = mBa
FAB – mBg sin θ = mBa
FAB = mBa + mBg sin θ ............... Pers. (2)
Karena FAB = FBA, maka kita dapat mensubtitusikan persamaan (2) ke dalam persamaan (1) sebagai berikut.
F – mAg sin θ – (mBa + mBg sin θ) = mAa
F – mAg sin θ – mBa – mBg sin θ = mAa
F – mAg sin θ – mBg sin θ = mAa + mBa
F – g sin θ(mA + mB) = (mA + mB)a
a = [F – g sin θ(mA + mB)]/(mA + mB)
a = [F/(mA + mB)] – g sin θ ............... Pers. (3)
Dengan mensubtitusikan nilai-nilai yang diketahui dalam soal ke dalam persamaan (3), maka kita peroleh besar percepatan kedua balok sebagai berikut.
a = [480/(40 + 20)] – (10) sin 37°
a = (480/60) – (10)(0,6)
a = 8 – 6
a = 2 m/s2
Jadi, besar percepatan kedua balok adalah 2 m/s2. Untuk menentukan gaya kontak antara balok A dan B, kita subtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (2) sebagai berikut.
FAB = mBa + mBg sin θ
FAB = (20)(2) + (20)(10)(sin sin 37°)
FAB = 40 + (200)(0,6)
FAB = 40 + 120
FAB = 160 N
Dengan demikian, besar gaya kontak antara balok A dan balok B adalah 160 N.
Catatan Penting:a = [F/(mA + mB)] – g sin θRumus percepatan di atas berlaku untuk semua model soal dua benda yang bersentuhan di bidang miring licin dengan sudut kemiringan tertentu.
Contoh Soal #2
Tiga buah balok dengan massa masing-masing m1 = 2 kg, m2 = 3 kg dan m3 = 5 kg terletak pada lantai datar dan disusun seperti pada gambar di bawah ini. Sebuah gaya F horizontal sebesar 100 N dikenakan pada balok 1. Apabila koefisien gesek kinetik ketiga balok dengan lantai adalah sama, sebesar 0,2 maka tentukanlah
■ Percepatan ketiga balok
■ Gaya kontak antara balok 1 dan balok 2
■ Gaya kontak antara balok 2 dan balok 3
Jawab
Diketahui:
m1 = 2kg
m2 = 3 kg
m3 = 5 kg
F = 100 N
μk = 0,2
g = 10 m/s2
Ditanyakan: Percepatan dan gaya kontak.
Seperti pada penyelesaian soal pertama, langkah awal yang wajib kita lakukan adalah menggambarkan garis-garis gaya yang bekerja pada masing-masing balok secara terpisah seperti yang ditunjukkan pada gambar di bawah ini.
Mungkin kalian sedikit bingung dengan banyaknya gaya yang bekerja pada masing-masing balok terutama vektor gaya yang bewarna merah. Oleh karena itu, supaya kalian bisa paham, berikut ini adalah keterangan masing-masing gaya tersebut.
F12 = gaya aksi yang diberikan balok 1 kepada balok 2
F21 = gaya reaksi yang diberikan balok 2 kepada balok 1
F23 = gaya aksi yang diberikan balok 2 kepada balok 3
F32 = gaya reaksi yang diberikan balok 3 kepada balok 2
Berdasarkan keterangan tersebut, dapat kita simpulkan bahwa:
■ F12 dan F21 merupakan gaya kontak antara balok 1 dan balok 2 sehingga
F12 = F21
■ F23 dan F32 merupakan gaya kontak antara balok 2 dan balok3 sehingga
F23 = F32
Kemudian, untuk menentukan besar percepatan ketiga balok dan juga gaya kontak, kita tinjau persamaan gerak masing-masing balok menggunakan Hukum I dan II Newton sebagai berikut.
■ Tinjau Balok 1
ΣFY = 0
N1 – w1 = 0
N1 = w1
N1 = m1g
ΣFX = ma
F – f1 – F21 = m1a
F – μkN1 – F21 = m1a
F – μkm1g – F21 = m1a ............... Pers. (4)
■ Tinjau Balok 2
ΣFY = 0
N2 – w2 = 0
N2 = w2
N2 = m2g
ΣFX = ma
F12 – f2 – F32 = m2a
F12 – μkN2 – F32 = m2a
F12 – μkm2g – F32 = m2a ............... Pers. (5)
■ Tinjau Balok 3
ΣFY = 0
N3 – w3 = 0
N3 = w3
N3 = m3g
ΣFX = ma
F23 – f3 = m3a
F23 – μkN3 = m3a
F23 – μkm3g = m3a
F23 = m3a + μkm3g ............... Pers. (6)
Karena F23 = F32, maka kita dapat mensubtitusikan persamaan (6) ke dalam persamaan (5) sebagai berikut.
F12 – μkm2g – F32 = m1a
F12 – μkm2g – (m3a + μkm3g) = m2a
F12 = m2a + m3a + μkm2g + μkm3g ............... Pers. (7)
Karena F12 = F21, maka kita dapat mensubtitusikan persamaan (7) ke dalam persamaan (4) sebagai berikut.
F – μkm1g – F21 = m1a
F – μkm1g – (m2a + m3a + μkm2g + μkm3g) = m1a
F – μkm1g – m2a – m3a – μkm2g – μkm3g = m1a
F – μkm1g – μkm2g – μkm3g = m1a + m2a + m3a
F – μkg(m1 + m2 + m3) = (m1 + m2 + m3)a
a = [F – μkg(m1 + m2 + m3)]/(m1 + m2 + m3)
a = [F/(m1 + m2 + m3)] – μkg ............... Pers. (8)
Kemudian kita masukkan nilai-nilai yang diketahui dalam soal ke dalam persamaan (8) sehingga kita peroleh besar percepatan, yaitu sebagai berikut.
a = [100/(2 +3 + 5)] – (0,2)(10)
a = (100/10) – 2
a = 10 – 2
a = 8 m/s2
Jadi besar percepatan ketiga balok adalah 8 m/s2. Lalu untuk menentukan besar gaya kontak antara balok 1 dan balok 2, kita dapat mensubtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (4) sebagai berikut.
F – μkm1g – F21 = m1a
100 – (0,2)(2)(10) – F21 = (2)(8)
100 – 4 – F21 = 16
96 – F21 = 16
F21 = 96 – 16
F21 = 80 N
Jadi besar gaya kontak antara balok 1 dan balok 2 adalah 80 N. Dan terakhir, untuk menentukan besar gaya kontak antara balok 2 dan balok 3, kita subtitusikan nilai percepatan 8 m/s2 ke dalam persamaan (6) sebagai berikut.
F23 = m3a + μkm3g
F23 = (5)(8) + (0,2)(5)(10)
F23 = 40 + 10
F23 = 50 N
Dengan demikian, besar gaya kontak antara balok 2 dan balok 3 adalah 50 N.
Catatan Penting:a = [F/(m1 + m2 + m3)] – μkgRumus percepatan di atas berlaku untuk semua model soal tiga benda yang bersentuhan di bidang datar kasar dengan koefisien gesek ketiga benda dengan lantai sama. Sedangkan rumus percepatan untuk tiga benda yang bersentuhan di bidang datar licin adalah sebagai berikut.a = F/(m1 + m2 + m3)Penurunan kedua rumus percepatan di atas, selengkapnya dapat kalian pelajari dalam artikel tentang Hukum Newton pada Gerak 3 Benda yang Bersentuhan di Bidang Datar.
Demikianlah artikel tentang contoh soal dan pembahasan tentang gaya aksi-reaksi atau gaya kontak (Hukum 3 Newton) beserta gambar ilustrasi dan diagram gayanya. Semoga dapat bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, huruf maupun angka dalam perhitungan mohon dimaklumi. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.



mantap mas, sangat bermanfaat
ReplyDeletesama-sama kak Malik...
DeleteKak saya mau tanya soal ini kak
ReplyDelete1.balok a dan balok b terletak di atas bidang miring licin dengan sudut kemiringan sebesar teta. Masa balok a didorong dengan gaya f sehingga K2 balok bergerak ke atas seperti yang diperhatikan pada gambar ...
Tentukan percepatan gerak K2 balok tersebut
Terimakasih kak penjelasannya sangat lengkap :")
ReplyDelete