10 Contoh Soal Pemantulan Cahaya Beserta Jawabannya
https://www.fisikabc.com/2018/04/contoh-soal-dan-jawaban-pemantulan-cahaya.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Pemantulan cahaya atau refleksi adalah proses terpancarnya kembali cahaya dari permukaan benda yang terkena cahaya. Peristiwa pemantulan cahaya dapat terjadi pada permukaan cermin, baik itu cermin datar, cermin cekung, maupun cermin cembung. Dalam konsep pemantulan cahaya, tentunya tidak terlepas dari Hukum Snellius tentang pemantulan cahaya. Adapun rumusan Hukum Pemantulan Cahaya Snellius antara lain sebagai berikut.
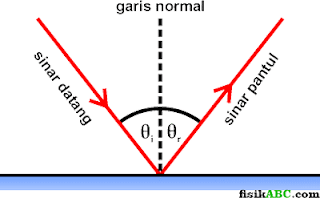
□ Sinar datang, garis normal dan sinar pantul terletak pada satu bidang datar.
□ Sudut datang sama dengan sudut pantul. Secara matematis, persamaan sudut datang dan sudut pantul dituliskan dalam bentuk rumus berikut.
θi = θr
|
□ Sinar datang tegak lurus cermin akan dipantulkan kembali.
Nah, pada kesempatan kali ini kita akan membahas kumpulan contoh soal yang berhubungan dengan peristiwa pemantulan cahaya lengkap dengan pembahasannya. Untuk itu, silahkan kalian simak baik-baik penjelasan berikut ini. selamat belajar dan semoga bisa paham.
1. Dua buah cermin disusun seperti pada gambar di bawah ini. Apabila sinar datang pada cermin A memiliki sudut datang 40°, tentukanlah arah sinar pantul (sudut pantul) oleh cermin B.
Gambar
Jawab
Di titik A, i adalah sudut datang = 40°.
Berdasarkan Hukum Pemantulan, i = r maka r = 40°.
∠P = ∠BAO = ∠NAO − ∠r = 90° − 40° = 50°
Besar sudut r’ dapat dicari dari
⇔ ∠r’ + ∠P + ∠AOB = 180°
⇔ ∠r’ + 50° + 90° = 180°
⇔ ∠r’ + 140° = 180°
⇔ ∠r’ = 180° − 140°
⇔ ∠r’ = 40°
Besarnya sudut i1 dapat dicari dari
⇔ ∠r’ + ∠i1 = 90°
⇔ 40° + ∠i1 = 90°
⇔ ∠i1 = 90° − 40°
⇔ ∠i1 = 50°
∠i1 merupakan sudut datang terhadap cermin B.
Berdasarkan Hukum Pemantulan, di titik B berlaku:
∠i1 = ∠r1
∠r1 = 50°
Jadi, arah sinar pantul oleh cermin B membentuk sudut 50° terhadap garis normal.
2. Hitunglah panjang minimum suatu cermin yang dibutuhkan agar seorang penari adat yang tinggi badannya 160 cm dapat melihat seluruh tubuhnya.
Jawab:
Panjang minimum cermin yang dibutuhkan adalah setengah kali tinggi badan seseorang, sehingga:
Panjang cermin minimum = ½ × tinggi badan
Panjang cermin minimum = ½ × (160 cm)
Panjang cermin minimum = 80 cm
Jadi, penari adat tersebut dapat melihat seluruh tubuhnya apabila berdiri di depan cermin datar yang panjangnya 80 cm.
3. Sebuah benda diletakkan di antara dua buah cermin datar yang disusun sedemikian rupa sehingga membentuk sudut sebesar 45° satu sama lain. Berapakah jumlah bayangan benda yang terbentuk?
Penyelesaian:
Diketahui : θ = 45°
Ditanya : n = ?
Jawab:
n = (360°/45°) – 1
n = 8 – 1
n = 7
Jadi, banyaknya bayangan yang terbentuk adalah 7 buah bayangan.
Catatan Penting:
Jika hasil pembagian merupakan bilangan desimal, maka sebelum atau sesudah dikurang 1, harus dibulatkan ke bawah. Sebagai contoh, apabila sudut apit kedua cermin sebesar 50°, maka jumlah bayangan adalah sebagai berikut:
n = (360°/50°) – 1
n = 7,2 – 1
n = 6,2
n = 6
|
4. Benda setinggi 6 cm berada di depan cermin cekung yang berjari-jari 30 cm. bila jarak benda ke cermin 20 cm, maka tentukanlah jarak bayangan, perbesaran bayangan, tinggi bayangan dan sifat bayangan.
Penyelesaian:
Diketahui:
h = 6 cm
R = 30 cm
s = 20 cm
f = ½ R = 15 cm
Ditanyakan: s’, M, h dan sifat bayangan.
Jawab
■ Jarak bayangan
1/f = 1/s + 1/s’
1/15 = 1/20 + 1/s’
1/s’ = 1/15 – 1/20
1/s’ = 4/60 – 3/60
1/s’ = 1/60
s' = 60 cm
Jadi, bayangan benda berada di depan cermin dengan jarak 60 cm.
■ Perbesaran bayangan
M = |s’/s|
M = |60/20|
M = 3x
Jadi, perbesaran bayangan benda adalah 3x dari benda aslinya.
■ Tinggi Bayangan
M = h’/h
3 = h’/6
h' = 3 × 6
h' = 18 cm
Jadi, tinggi bayangan benda adalah 18 cm.
■ Sifat Bayangan
Dari perhitungan di atas kita peroleh data berikut.
s' = 60 cm
h' = 18 cm
• s’ bernilai positif maka bayangan berada di depan cermin sehingga bersifat nyata dan terbalik.
• h’ > h sehingga bayangan bersifat diperbesar.
Dengan demikian, sifat bayangan yang terbentuk adalah nyata, terbalik dan diperbesar.
5. Benda setinggi 10 cm, berada di depan cermin cembung yang memiliki jari-jari 80 cm. Bila jarak benda 60 cm, maka tentukan letak bayangan, perbesaran bayangan dan tinggi bayangan!
Penyelesaian:
Diketahui:
h = 10 cm
s = 60 cm
R = 80 cm = −80 cm (dibelakang cermin)
f = ½R = ½(−80 cm) = −40 cm
Ditanyakan: s’, M dan h
Jawab:
■ Jarak bayangan
1/−f = 1/s + 1/s’
1/−40 = 1/60 + 1/s’
1/s’ = 1/−40 − 1/60
1/s’ = −3/120 − 2/120
1/s’ = −5/120
s' = 120/−5
s' = −24 cm
Jadi, bayangan benda berada di belakang cermin pada jarak 24 cm.
■ Perbesaran bayangan
M = |s’/s|
M = |−24/60|
M = 0,4x
Jadi, bayangan benda mengalami perbesaran 0,4x (bayangan benda lebih kecil).
■ Tinggi Bayangan
M = h’/h
0,4 = h’/10
h' = 0,4 × 10
h' = 4 cm
Jadi, tinggi bayangan benda adalah 4 cm.
6. Sebuah benda diletakkan di depan cermin cembung sedemikian rupa sehingga besar bayangannya 0,5 kali. Jika bayangan yang terbentuk terletak 0,55 cm di belakang cermin, hitunglah jarak fokus cermin cembung tersebut.
Penyelesaian:
Diketahui:
M = 0,5
s' = −0,55 cm
Ditanyakan: f
Jawab:
Pertama, kita tentukan terlebih dahulu jarak benda (s) dari cermin menggunakan rumus perbesaran bayangan berikut.
M = |s’/s|
0,5 = |−0,55/s|
0,5 = 0,55/s
s = 0,55/0,5
s = 1,1 cm
Kedua, kita tentukan jarak fokus (f) menggunakan rumus hubungan jarak benda dan jarak bayangan dengan jarak fokus berikut ini.
1/f = 1/s + 1/s’
1/f = 1/1,1 + 1/−0,55
1/f = 1/1,1 + −2/1,11
1/f = −1/1,11
f = 1,11/−1
f = −1,11 cm
jadi, jarak fokus cermin cembung tersebut adalah 1,11 cm di belakang cermin.
7. Seratus centimeter di depan cermin cembung ditempatkan sebuah benda. Titik pusat kelengkungan cermin 50 cm. Tentukan jarak bayangan ke cermin dan perbesaran bayangan itu.
Penyelesaian:
Diketahui:
s = 100 cm
R = −50 cm
Ditanyakan: s’ dan M
Jawab:
■ Jarak bayangan dapat ditentukan dengan menggunakan rumus berikut.
2/R = 1/s + 1/s’
2/−50 = 1/100 + 1/s’
1/s’ = 2/−50 − 1/100
1/s’ = −4/100 − 1/100
1/s’ = −5/100
s' = 100/−5
s' = −20 cm
jadi, jarak bayangan adalah 20 cm di belakang cermin cembung.
■ Perbesaran bayangan dapat ditentukan dengan menggunakan rumus berikut:
M = |s’/s|
M = |−20/100|
M = 0,2x
Jadi, bayangan benda mengalami perbesaran 0,2x benda sebenarnya.
8. Dimanakah sebuah benda kecil harus diletakkan di muka cermin cekung (f = 10 cm) agar diperoleh perbesaran 5 kali?
Penyelesaian:
Diketahui:
f = 10 cm
M = 5
Ditanyakan: s
Jawab:
Dari rumus perbesaran, kita peroleh perbandingan antara jarak benda (s) dengan jarak bayangan (s’) yaitu sebagai berikut.
M = |s’/s|
5 = s’/s
s' = 5s
Kemudian kita gunakan rumus jarak fokus untuk menentukan nilai s, yaitu sebagai berikut.
1/f = 1/s + 1/s’
1/10 = 1/s + 1/5s
1/10 = 5/5s + 1/5s
1/10 = 6/5s
5s/6 = 10
5s = 60
s = 60/5
s = 12 cm
Jadi, benda tersebut harus diletakkan didepan cermin cekung sejauh 12 cm.
9. Sebuah benda dengan tinggi 9 cm berada pada jarak 30 cm dari cermin cembung yang jari-jari kelengkungannya 30 cm. Berapakah tinggi bayangannya?
Penyelesaian:
Diketahui:
h = 9 cm
s = 30 cm
R = −30 cm
Ditanyakan: h’
Jawab:
Pertama, kita tentukan dahulu jarak bayangan (s’) dengan rumus sebagai berikut.
2/R = 1/s + 1/s’
2/−30 = 1/30 + 1/s’
1/s’ = 2/−30 − 1/30
1/s’ = −2/30 − 1/30
1/s’ = −3/30
s' = 30/−3
s' = −10 cm
Kedua, kita tentukan tinggi bayangan dengan menggunakan persamaan perbesaran bayangan, yaitu sebagai berikut.
M = |s’/s| = |h’/h|
Maka
|s’/s| = |h’/h|
|−10/30| = |h’/9|
10/30 = h’/9
1/3 = h’/9
h' = 9/3
h’ = 3 cm
Dengan demikian, tinggi bayangannya adalah 3 cm.
10. Di dalam sebuah cermin cekung, bayangan kepala saya 3 kali besar kepala saya. Bila jarak antara saya dengan cermin cekung 15 cm, tentukan jari-jari kelengkungan cermin tersebut!
Penyelesaian:
Diketahui:
M = 3
s = 15 cm
Ditanyakan: R
Jawab:
Pertama, kita tentukan dahulu jarak bayangan (s’) menggunakan rumus perbesaran berikut ini.
M = |s’/s|
3 = s’/15
s' = 3 × 15
s’ = 45 cm
Kedua, kita tentukan jari-jari kelengkungan cermin dengan menggunakan rumus berikut ini.
2/R = 1/s + 1/s’
2/R = 1/15 + 1/45
2/R = 3/45 + 1/45
2/R = 4/45
R/2 = 45/4
R/2 = 11,25
R = 11,25 × 2
R = 22,5 cm
Jadi, panjang jari-jari kelengkungan cermin tersebut adalah 22,5 cm.