Ringkasan Materi Pemantulan dan Pembiasan Cahaya Lengkap dengan Contoh Soal
https://www.fisikabc.com/2018/05/materi-pemantulan-dan-pembiasan-cahaya.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Dalam optika geometri, pemantulan dan pembiasan cahaya merupakan elemen yang sangat penting untuk dipahami. Terutama dalam memahami prinsip kerja alat-alat optik seperti lup, mikroskop, teleskop, kamera, periskop dan sebagainya. Nah, pada kesempatan kali ini, penulis akan menyajikan ringkasan materi tentang pemantulan dan pembiasan cahaya. Untuk itu, silahkan kalian simak baik-baik penjelasan berikut ini.
Materi Pemantulan Cahaya
Apa itu Pemantulan Cahaya?
Pemantulan atau refleksi cahaya adalah proses terpancarnya kembali cahaya dari permukaan benda yang terkena cahaya. Peristiwa pemantulan cahaya secara mudah dapat kita amati pada permukaan benda yang mengkilap seperti cermin atau logam.
Macam-Macam Pemantulan Cahaya
Pemantulan cahaya dibedakan menjadi dua, yaitu sebagai berikut.
■ Pemantulan baur (difus) adalah pemantulan cahaya yang terjadi pada pemukaan benda yang tidak rata, di mana berkas sinar (cahaya) pantulnya mempunyai arah yang tidak teratur (baur). Contohnya, pemantulan cahaya pada tembok, kayu, batu, tanah dan sebagainya.
■ Pemantulan teratur adalah pemantulan cahaya yang terjadi pada permukaan yang rata, di mana berkas sinar (cahaya) pantulnya mempunyai arah yang teratur (sama). Pemantulan teratur bersifat menyilaukan, namun mampu menghasilkan bayangan yang jelas. Pemantulan teratur bisa terjadi pada cermin.
Hukum Snellius Pada Pemantulan Cahaya
Adapun rumusan hukum pemantulan cahaya yang dikemukakan oleh Willebrord Snellius adalah sebagai berikut.
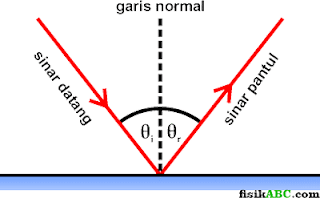
1) Sinar datang, garis normal dan sinar pantul terletak pada satu bidang datar.
2) Sudut datang sama dengan sudut pantul. Secara matematis, persamaan sudut datang dan sudut pantul dituliskan dalam bentuk rumus berikut.
θi = θr
|
3) Sinar datang tegak lurus cermin akan dipantulkan kembali.
Contoh Soal:
Dua buah cermin disusun seperti pada gambar di bawah ini. Apabila sinar datang pada cermin A memiliki sudut datang 40°, tentukanlah arah sinar pantul (sudut pantul) oleh cermin B.
Jawab
Di titik A, i adalah sudut datang = 40°.
Berdasarkan Hukum Pemantulan, i = r maka r = 40°.
∠P = ∠BAO = ∠NAO − ∠r = 90° − 40° = 50°
Besar sudut r’ dapat dicari dari
⇔ ∠r’ + ∠P + ∠AOB = 180°
⇔ ∠r’ + 50° + 90° = 180°
⇔ ∠r’ + 140° = 180°
⇔ ∠r’ = 180° − 140°
⇔ ∠r’ = 40°
Besarnya sudut i1 dapat dicari dari
⇔ ∠r’ + ∠i1 = 90°
⇔ 40° + ∠i1 = 90°
⇔ ∠i1 = 90° − 40°
⇔ ∠i1 = 50°
∠i1 merupakan sudut datang terhadap cermin B.
Berdasarkan Hukum Pemantulan, di titik B berlaku:
∠i1 = ∠r1
∠r1 = 50°
Jadi, arah sinar pantul oleh cermin B membentuk sudut 50° terhadap garis normal.
Materi Pembiasan Cahaya
Apa itu Pembiasan Cahaya?
Pembiasan atau difraksi cahaya adalah adalah peristiwa pembelokan arah cahaya ketika melewati bidang batas antara dua medium yang berbeda kerapatan optiknya. Pembiasan cahaya terjadi akibat kecapatan cahaya berbeda pada setiap medium.
Syarat Terjadinya Pembiasan Cahaya
Ada dua syarat terjadinya proses pembiasan cahaya, yaitu:
□ Cahaya merambat melalui dua medium yang memiliki perbedaan kerapatan optik, misalnya udara dengan air, udara dengan kaca, air dengan kaca, dan sebagainya.
□ Cahaya yang datang harus miring pada batas dua medium, karena jika tegak lurus maka tidak akan mengalami proses pembiasan.
□ Cahaya yang datang dari medium lebih rapat menuju medium kurang rapat (ex. kaca ke udara) harus menghasilkan sudut bias lebih kecil dari 90°. Hal ini karena jika sinar bias sama dengan 90° maka cahaya tidak akan memasuki medium kedua. Sedangkan jika sudut bias lebih besar dari 90° maka akan terjadi peristiwa pemantulan sempurna.
Hukum Snellius Pada Pembiasan Cahaya
Adapun rumusan hukum pembiasan cahaya yang dikemukakan oleh Willebrord Snellius adalah sebagai berikut.
1) Sinar datang, garis normal dan sinar bias terletak dalam satu bidang datar.
2) Perbandingan sinus sudut datang dengan sinus sudut bias pada dua medium yang berbeda merupakan bilangan tetap.
Secara matematis, pernyataan Hukum Snellius yang kedua di atas dapat dituliskan dalam bentuk persamaan berikut.
sin i1
|
=
|
sin i2
|
=
|
sin i3
|
sin r1
|
sin r2
|
sin r3
|
sin i
|
=
|
Tetap
|
…….. pers. (1)
|
sin r
|
Tetapan atau konstanta tersebut disebut dengan indeks bias relatif suatu medium terhadap medium lain. Jika sinar datang dari medium 1 ke medium 2, maka indeks bias relatif medium 2 terhadap medium 1 ditulis sebagai berikut.
n21
|
=
|
n2
|
n1
|
Dengan demikian, persamaan (1) di atas dapat ditulis ulang sebagai berikut.
sin i
|
=
|
n21
|
sin r
|
sin i
|
=
|
n2
|
…….. pers. (2)
|
sin r
|
n1
|
Sehingga kita peroleh rumus hubungan antara sudut datang, sudut bias dan indeks bias medium sebagai berikut.
n1 sin i = n2 sin r
|
Keterangan:
n1 = indeks bias mutlak medium 1
n2 = indeks bias mutlak medium 2
n21 = indeks bias relatif medium 2 terhadap medium 1
i = sudut datang pada medium 1
r = sudut bias pada medium 2
Contoh Soal:
Seseorang menyinari sebuah kaca tebal dengan sudut 30° terhadap garis normal. Jika cepat rambat cahaya di dalam kaca adalah 2 × 108 m/s, tentukan indeks bias kaca dan sudut biasnya.
Penyelesaian:
Diketahui:
θi = 30°
v2 = 2 × 108 m/s
Ditanyakan: n2 (indeks bias kaca) dan θr
Jawab:
■ Untuk mencari indeks bias kaca, gunakan persamaan:
n
|
=
|
c
|
=
|
3 × 108 m/s
|
=
|
1,5
|
v
|
2 × 108 m/s
|
Jadi, indeks bias kaca adalah 1,5
■ Untuk mencari sudut bias, gunakan hukum Snellius.
sin i
|
=
|
n2
|
sin r
|
n1
|
sin 30°
|
=
|
1,5
|
sin r
|
1
|
sin r
|
=
|
0,5
|
1,5
|
sin r
|
=
|
0,33
|
r
|
=
|
sin−1 (0,33)
|
r
|
=
|
19,27°
|
Jadi, besar sudut biasnya adalah 19,27°.
Hukum-Hukum Lain yang Berlaku Pada Pembiasan Cahaya
Selain kedua pernyataan Hukum Snellius di atas, masih ada hal lain yang berlaku pada peristiwa pembiasan cahaya, yaitu sebagai berikut.
1) Jika sinar datang dari medium kurang rapat ke medium lebih rapat, sinar akan dibiaskan mendekati garis normal. Ini berarti, sudut bias lebih kecil daripada sudut datangnya (r < i).
2) Jika sinar datang dari medium lebih rapat ke medium kurang rapat, cahaya akan dibiaskan menjauhi garis normal. Jadi, sudut datang lebih kecil dari sudut bias (i < r).
3) Jika sinar datang tegak lurus batas dua medium, maka sinar tidak dibiaskan melainkan diteruskan.
Apa itu Indeks Bias?
Indeks bias adalah perbandingan kelajuan cahaya di udara dengan kelajuan cahaya di dalam suatu zat (ex. air, kaca, udara, dsb.). Semakin besar indeks bias suatu zat maka semakin besar cahaya dibelokkan/dibiaskan oleh zat tersebut. Besarnya pembiasan juga bergantung pada panjang gelombang cahaya.
Apa itu Indeks Bias Mutlak?
Indeks bias mutlak adalah perbandingan cepat rambat cahaya di ruang hampa dengan cepat rambat cahaya di dalam medium. Indeks bias mutlak suatu medium dapat dicari dengan persamaan berikut.
n
|
=
|
c
|
v
|
Keterangan:
n = indeks bias mutlak medium
c = cepat rambat cahaya di ruang hampa (3 × 108 m/s)
v = cepat rambat cahaya di dalam medium.
Contoh Soal:
Cahaya merambat dari udara ke air. Bila cepat rambat cahaya di udara adalah 3 × 108 m/s dan indeks bias air 4/3, maka tentukanlah cepat rambat cahaya di air!
Penyelesaian:
Diketahui:
c = 3 × 108 m/s
nair = 4/3
Ditanyakan: vair
Jawab:
nair
|
=
|
c
|
vair
|
Maka cepat rambat cahaya di air dirumuskan sebagai berikut.
vair
|
=
|
c
|
nair
|
vair
|
=
|
3 × 108 m/s
|
4/3
|
vair = 2,25 × 108 m/s
Jadi, cepat rambat cahaya di dalam air adalah 2,25 × 108 m/s.
Apa itu Indeks Bias Relatif?
Indeks bias relatif adalah perbandingan indeks bias mutlak dari dua buah medium yang berbeda. Jika cahaya datang dari medium 1 dengan indeks bias n1menuju medium 2 dengan indeks bias mutlak n2, maka indeks bias relatif medium 2 terhadap medium 1 dinyatakan dengan persamaan berikut.
n21
|
=
|
n2
|
n1
|
Dengan mensubtitusikan persamaan n = c/v, kita mendapat bentuk persamaan berikut ini.
n21
|
=
|
c/v2
|
c/v1
|
n21
|
=
|
v1
|
…….. pers. (3)
|
v2
|
Keterangan:
n21 = indeks bias relatif medium 2 terhadap medium 1
I = sudut datang
r = sudut bias
n1 = indeks bias medium 1
n2 = indeks bias medium 2
v1 = cepat rambat cahaya pada medium 1
v2 = cepat rambat cahaya pada medium 2
Contoh Soal:
Cahaya datang dari air ke kaca. Indeks bias air = 1,33, indeks bias kaca = 1,54. Hitunglah indeks bias relatif kaca terhadap air dan kecepatan cahaya di kaca jika kecepatan cahaya di air sebesar 2,25 × 108 m/s.
Penyelesaian:
Diketahui:
nair = 1,33
nkaca = 1,54
vair = 2,25 × 108 m/s
Ditanyakan: nka (indeks bias relatif kaca terhadap air) dan vkaca
Jawab:
■ Indeks bias relatif kaca terhadap air
nka
|
=
|
nkaca
|
nair
|
nka
|
=
|
1,54
|
1,33
|
nka
|
=
|
1,16
|
■ Kecepatan cahaya di dalam kaca
nair
|
=
|
vkaca
|
nkaca
|
vair
|
1,33
|
=
|
vkaca
|
1,54
|
2,25 × 108
|
vkaca
|
=
|
1,33
|
×
|
2,25 × 108
|
1,54
|
vkaca
|
=
|
1,94 × 108 m/s
|
Hubungan Indeks Bias dengan Cepat Rambat Cahaya, Panjang Gelombang dan Frekuensi
Untuk menentukan hubungan antara indeks bias dengan cepat rambat cahaya, kita dapat mensubtitusikan persamaan (3) ke dalam persamaan (2) sehingga kita peroleh persamaan berikut.
n2
|
=
|
v1
|
=
|
sin i
|
………. Pers. (4)
|
n1
|
v2
|
sin r
|
Keterangan:
n1 = indeks bias mutlak medium-1
n2 = indeks bias mutlak medium-2
n1,2 = indeks bias medium-2 relatif terhadap medium-1
v1 = cepat rambat cahaya pada medium-1
v2 = cepat rambat cahaya pada medium-2
i = sudut datang di medium-1
r = sudut bias di medium-2
Ingat bahwa v = λf, dengan f = frekuensi cahaya dan λ = panjang gelombang. Dengan demikian, apabila kita subtitusikan v = λf ke dalam persamaan (3), maka kita peroleh rumus hubungan antara indeks bias medium, frekuensi dan panjang gelombang sebagai berikut.
n1, 2
|
=
|
λ1 × f
|
λ2 × f
|
n1, 2
|
=
|
λ1
|
………. Pers. (5)
|
λ2
|
Keterangan:
n1,2 = indeks bias medium
λ1 = panjang gelombang cahaya pada medium-1
λ2 = panjang gelombang cahaya pada medium-2
f = frekuensi cahaya
Contoh Soal:
Suatu berkas cahaya dengan panjang gelombang 6 × 10-7 m datang dari udara ke balok kaca yang indeks biasnya 1,5. Hitunglah panjang gelombang dalam kaca.
Penyelesaian:
Diketahui:
λ1 = 6 × 10-7 m (udara)
n1 = 1 (udara)
n2 = 1,5 (kaca)
Ditanyakan: λ2 (kaca)
Jawab:
Panjang gelombang cahaya di dalam medium kaca, dapat kita tentukan dengan mensubtitusikan persamaan (9) ke persamaan (5) sebagai berikut.
n2
|
=
|
λ1
|
n1
|
λ2
|
1,5
|
=
|
6 × 10-7
|
1
|
λ2
|
λ2
|
=
|
6 × 10-7
|
=
|
4 × 10-7
|
1,5
|
Jadi, panjang gelombang cahaya ketika melewati medium kaca adalah 4 × 10-7 m.
Apa itu Pemantulan Sempurna?
Bila sinar datang dari medium lebih rapat menuju medium kurang rapat, sinar akan dibiaskan menjauhi garis normal. Jika sudut datangnya dirubah, pada saat sudut datang membentuk sudut bias 90o, sudut datang ini disebut sudut kritis (batas). Untuk sudut datang melebihi sudut kritis, berkas sinar tidak dibiaskan lagi melainkan dipantulkan seluruhnya. Peristiwa ini disebut pemantulan sempurna atau pemantulan total.
Syarat Terjadinya Pemantulan Sempurna
pemantulan sempurna atau pemantulan total hanya akan terjadi apabila memenuhi dua syarat sebagai berikut.
□ Cahaya datang dari medium lebih rapat ke medium kurang rapat atau dengan kata lain, indeks bias medium pertama harus lebih besar dari indeks bias medium kedua (n1 > n2).
□ Sudut datang harus lebih besar daripada sudut kritis. Misalnya, jika sudut datang adalah i dan sudut kritis adalah ik maka pada pemantulan sempurna berlaku i > ik.
Apa itu Sudut Kritis Pada Pemantulan Sempurna?
Jika sudut sinar datang dari medium pertama mempunyai sudut bias 90° disebut sudut kritis (sudut batas) dan ditulis ik, maka menurut Hukum Snellius untuk pembiasan cahaya, berlaku persamaan berikut.
n1 sin ik = n2 sin r
n1 sin ik = n2 sin 90°
n1 sin ik = n2 (1)
n1 sin ik = n2
sin ik
|
=
|
n2
|
n1
|
ik
|
=
|
sin-1
|
n2
|
n1
|
Keterangan:
ik = sudut kritis (sudut batas)
n1 = indeks bias medium pertama
n2 = indeks bias medium kedua
n1 > n2
Contoh Soal:
Hitunglah sudut kritis berlian yang memiliki indeks bias mutlak 2,417 pada saat diletakkan di udara.
Jawab:
Diketahui:
n2 = 1 (udara)
n1 = 2,417 (berlian)
Maka sudut kritisnya dapat dihitung dengan rumus berikut.
ik
|
=
|
sin-1
|
1
|
2,417
|
ik
|
=
|
sin-1 (0,414)
|
ik
|
=
|
24,4°
|
Jadi, sudut kritis berlian tersebut adalah 24,4°.